Oct 10, 2008 I am asked to find the second derivative of the volume of a cube with respect to the length of a side. Would my initial f(x)=x 3 /x?? Than just follow with the quotient rule to get f (2) (x)? The derivative of a field with respect to a fixed position in space is called the Eulerian derivative while the derivative following a moving parcel is called the advective or material ('Lagrangian' ) derivative. The material derivative is defined as the nonlinear operator.
Density of States Derivation. The density of states gives the number of allowed electron (or hole) states per volume at a given energy. It can be derived from basic quantum mechanics. Electron Wavefunction. The position of an electron is described by a wavefunction.
Example: a function for a surface that depends on two variables x and yWhen we find the slope in the x direction (while keeping y fixed) we have found a partial derivative.Or we can find the slope in the y direction (while keeping x fixed).Here is a function of one variable (x):f(x) = x 2And its (using the ):f’(x) = 2xBut what about a function of two variables (x and y):f(x,y) = x 2 + y 3To find its partial derivative with respect to x we treat y as a constant (imagine y is a number like 7 or something):f’ x = 2x + 0 = 2x. Example: f(x,y) = y 3sin(x) + x 2tan(y)It has x's and y's all over the place!
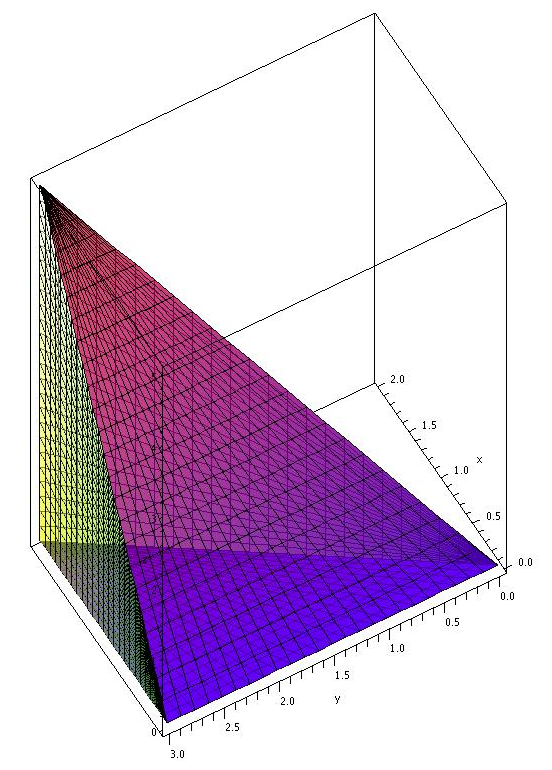
So let us try the letter change trick.With respect to x we can change 'y' to 'k':f(x,y) = k 3sin(x) + x 2tan( k)f’ x = k 3cos(x) + 2x tan(k)But remember to turn it back again!f’ x = y 3cos(x) + 2x tan(y)Likewise with respect to y we turn the 'x' into a 'k':f(x,y) = y 3sin( k) + k 2tan(y)f’ y = 3y 2sin(k) + k 2sec 2(y)f’ y = 3y 2sin(x) + x 2sec 2(y)But only do this if you have trouble remembering, as it is a little extra work.
Consider a sphere of radius r, where you want to increase the volume very slightly. You can do this by adding a layer of paint, covering the entire surface area, with a tiny thickness dr.

The volume of paint you've added to the sphere is dV=(area).dr.Integrate both sides, which acts like adding infinitely many tiny layers. Start from radius 0 until you've built up a sphere of the desired size. The result is the volume formula, which you used as the starting point of your calculation.You can do exactly the same thing for the area of a circle: consider a circle, of radius r and circumference 2pi.r. Paint such a thin circular ring, of thickness dr. Repeat this process (integration), until you've made a (filled) disk of the desired radius. The area will be the integral of 2pi.r: pi.r 2.Obligatory thanks-for-the-gold edit: I'm glad that so many people have found my explanation useful. This gives me a bit of hope that I won't be a completely crappy teacher when I get that far in my career.
How To Find The Density Of A Cube
Fractals are often the limit of an infinite series of shapes, for example, the (or the Koch snowflake). I am going to use this 2D shape as an example, as the principles are the same as for 3D structures, but the reasoning is easier to follow.Each step brings us closer to the final form. The area increases with each step, but it is bounded (as the maximum distance from the center does not increase). It can be shown that a growing, bounded series of numbers have a limit, and that limit is taken as the area of the final shape.However, if you look at the length of the perimeter, it grow with a factor of 4/3 each step. This series does not have a finite limit - no matter what limit you try to set, for some step and for every step after that, the perimeter must be longer than the limit. If we are going to talk of the length of the perimeter of the final object, we have to set it to infinity, as no other number makes sense.edit: So, in a way, it is because that, if we have a structure with a finite volume and area, we can always create a structure with the same volume but a larger area. Fractals are the limit of such a series.
Derivative Of Density Of A Cube Formula
Thanks for the help. Also, there were people talking about Stokes' theorem elsewhere in this thread. I don't have the background to understand it well, but my impression is that it's a formal/rigorous version of this intuition.
You might be interested in it.Stokes' theorem says that the integral of a differential form ω over the boundary of some orientable manifold Ω is equal to the integral of its exterior derivative dω over the whole of Ω, i.e.Seems like what we're saying, since manifold is a dimensionally neutral word.